Overview
A guide for newbies to the way the dice rolls work in Blood Bowl.
Maths? WTF? This is a game…
Yes, maths. Understanding the maths behind your actions in Blood Bowl is fundamental to the risk management aspect of the game, and since that risk management is a really big aspect of the game that makes understanding the maths really important.
That said, we are all playing this game on computers, and computers are really really good at maths. If you really don’t want to know how it works but do want to be able to think through some scenarios in terms of probabilities, or maybe see just how lucky your one-turn-touchdown attempt really was, you can use a great tool from Elyoukey to do so: [link]
So, for those who really do want to understand what the hell is going on, here are some basics.
The Dice
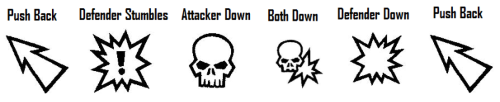
Dice are generally referred to by the number of sides that have and the number to be rolled, although this does not always hold. Many of the dice in Blood Bowl are dice with numbers on them, but there are also block dice which have symbols.
The following dice are used in Blood Bowl:
d6 – a standard 6 sided die
d8 – an 8 sided die
d68 – a d6 followed by a d8. This actually gives 48 possible results and is only used for casualty rolls
d3 – a six sided die with the result halved and rounded up: 1-2 = 1, 3-4 = 2, 5-6 = 3
Block Dice – standard 6-sided dice with symbols instead of numbers. The sides are as below:
Sometimes (e.g. Thrown Rock) a player on the pitch will need to be picked. That’s just a random selection of one of them and there are many ways to do this on TT which I won’t bother covering here because the roll itself is never combined with anything.
Rolling multiple dice is often called for, and the terminology normally (see the d68 exception above) will be
- [number of dice]d[sides on the dice]
So two six sided dice will be 2d6, for example.
Block dice can be rolled in ones, twos or threes. In some cases your opponent will choose the result and the dice will be displayed in red. The terminology is normally 1db, 2db and 3db if you are choosing, and -1db, -2db and -3db if your opponent is choosing. “Opponent choosing” blocks are often referred to as “uphill”. For more on how many block dice are used I strongly recommend reading The Art of Blocking[www.thenaf.net].
Basic Probabilities
The most commonly rolled dice in Blood Bowl are six-sided, be they numeric or block dice. To that end I will be concentrating mainly on those for the purposes of this guide. It’s fairly simply to substitute in another number of sides, though: wherever there is a 6 you could substitute in the number of sides on the die you are using.
The odds of any one side coming up when you roll a die are 1 in 6. This is what is known as an expected value. What it does not mean is that if you roll a single die 12 times you will get 2 6s. Dice don’t have a memory, so while 2 6s is the expected number it is not necessarily the actual number, and the difference between the two is known as variance. The same holds if you roll 12 different dice instead: you will not necessarily get the expected 2 6s.
It is this variance which means that anything is possible: it is possible to roll 6 6s, it is possible to roll a 1 and reroll into another 1, and it is possible for your minotaur to be hit by a goblin and die. Unlikely, perhaps, but possible.
Two dice being rolled are independent events. That means that the probability of any one specific roll coming up is the product of the probability of a number coming up on the first die and the probability of the number coming up on the second. Where this gets difficult is when we are looking for specific totals, because any one total can be made a number of ways with two dice. For example a 9 can be made with 6,3 4,5 5,4 and 3,6, which is 4 possibilities. 7 has 6 possible combinations.
One way to represent this is in a table of probabilities like the one below:
If the numbers across the top are the first die and the numbers down the left are the second then the ones in the middle of the table are the possible totals. With such a table we can easily count the number of times any one result comes up. For example, we can see there are 4 9s in that table, just as we said above.
Let’s say we are trying to break an armour of AV8 and want to know what the probability of that happening is. We need a 9 or more to do so, so we can count the number of times a 9 or more is in the table (it’s 10) and then the number of values in the table (36) and divide the former by the latter to give 10/36, which is a probability of 0.27778, or 27.778%. This means AV8 will normally be broken 27.778% of the time.
Block dice are very similar to d6 except two of the sides are the same. We can represent this with a similar table to the one above:
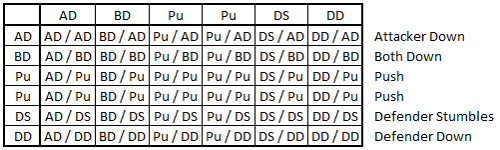
If we need to knock down a Minotaur with a Human Lineman we must make a -2d block. The best results for us are DS or DD since a BD result would be a turnover, and we don’t want that right now. There are 4 possible results from the 36 which work for us, which is 4/36 or 11.111% – likely quite a bit more probable than most people imagine.
Adding a further die to make a 3d block can be worked out two ways (3 if you include the Samba Action Calculator from the start of this guide!). You can either make a further table with all the 2d results along the top and put in a column for the extra die to give you all the possible results:

We can also, knowing the 2d probability, work out the 3d probability by multiplication. If instead of a Human Lineman blocking a Minotaur we use a Goblin we would make a -3d block. We know that a -2d block gives us a 4/36 chance to roll the required DS or DD, and since another DS or DD is required on the 3rd die, which is a 2/6 chance, multiplication gives us 4/36 * 2/6 = 8/216 = 3.7%
More to follow, including sequences and dependent rolls…